Question

in a circle , a chord 3 centimeters away from the center is 8 centimeters long . how long is a chord ,1.4 centimeters away from the center in the circle  ?

Answer 1

Let chord 8cm long meet the circle at at points A , B. Let Perpendicular from centre,say O, meet the above chord at C. Point C divides AB in two equal parts at C,i.e., AC = BC.
 Join OA. Then Triangle ACO have sides 4cm, 3cm and radius r. Then Radius = √(4² + 3²) = 5.

Now draw a chord 1.4cm from centre O. Let this chord meet circle at points D, E.
Let perpendicular 1.4cm long meet chord DE at F. Join OD which is = radius = 5.
Now in triangle ODF, OD = 5, OF = 1.4 . Hence DF = √(OD² - OF²) = √(5² - 1.4²) = 4.8. Hence length of the chord = 2x4.8 = 9.6cm
Complete triangle

Answer 2

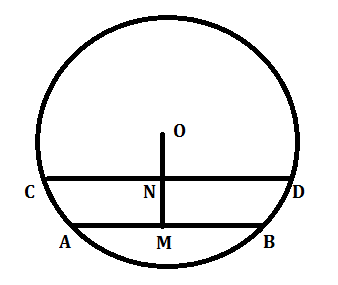
In the figure, OM = 3 cm

AB = 8 cm
Since OM bisects AB
Therefore, AM = BM = 4 cm
In the right triangle OMA
OM = 3 cm, AM = 4 cm
Therefore, by Pythagorean theorem, OA = 5 cm
That is, the radius of the circle = 5 cm

Now, ON = 1.4 cm
Let CN = x cm
By pythagorean theorem 
$(1.4)^2 + x^2 = 5^2$

$1.96 + x^2 = 25$

$x^2 = 23.04$

x = 4.8

Therefore, the length of the chord CD = 2x = 9.6 cm